Exact Cover, Dancing Links ve Sudoku Çözme

Donald Knuth tarafından geliştirilmiş olan "Dancing Links" algoritması, "exact cover" problemi ve bu probleme çevirilebilen sudoku gibi problemlerin çözümü için bir hayli etkin bir yöntem sunuyor. Bu yazıda, "exact cover" problemi, "dancing links" algoritması, sudoku probleminin exact cover problemine dönüştürülmesi konularından bahsedeceğim. Ayrıca, Ali Assaf tarafından "Algorithm X in 30 lines!" yazısında bahsedilen yönteme kısaca değineceğim.

Exact Cover (Birebir Örtme) Problemi

Matematikte, exact cover, bir X kümesinin, alt kümelerinden oluşan bir S koleksiyonun, öyle bir S* alt koleksiyonudur ki, X'in içindeki her eleman, S*'nin içindeki bir ve en fazla bir kümenin içinde bulunur.

Örneğin;

    X = {1,2,3,4,5}
    S = {{1,3},{1,4},{2,4,5}}

Kümelerinde, exact cover S* = {{1,3},{2,4,5}} olarak bulunur.

Exact cover problemi, NP-Complete bir problemdir. Donald Knuth tarafından geliştirilen "Algorithm X" algoritması, bu problemi çözmeye yarıyor. Ayrıca, Donald Knuth, dancing links dediği bir teknikle, bu algoritmanın nasıl çok verimli bir şekilde kodlanabileceğini göstermiş.

Dancing Links algoritmasına geçmeden önce, bu problemi bir matrix ile nasıl gösterebileceğimize bakalım;

    1 0 1 0 0 
    1 0 0 1 0
    0 1 0 1 1

Bu matrix'de sütunlar X'deki elemanları, satırlar ise, S koleksiyonundaki elemanları temsil ediyor. Bu durumda problem, buradaki satırlardan, her sütunda bir ve yalnızca bir 1 olacak şekilde bir grup seçmek halini alıyor. Dancing Link algoritmasında, bu matrix'i sparse matrix'e dönüştürüp, bu satırların seçimi yapılıyor.

Dancing Links Algoritması

Dancing Links, yukarıda bahsedilen problemin matrix'ini çifte linkli listelerden (C'deki double-linked list) oluşturmak fikrine dayanıyor. Bu tekniğin şöyle güzel bir yanı var ki, listeye eleman ekleyip çıkarmak çok kolay. Örneğin, diyelim ki, x, matrix'in içinde bir node, bunu matrix'den kaldırmak için bunun solundaki'nin sağını, bunun sağına eşitleyebilirsiniz.

x->left->right = x->right
x->right->left = x->left

Dikkat ederseniz, burada x üzerinde bir değişiklik yapılmıyor. Yani, x'in pointer'ları hala aynı yerde. Dolayısıyla, x'i matrix'deki eski yerine koymak da bu kadar basit:

x->right->left = x
x->left->right = x

Bu tekniğe dancing links denmesi, algoritmanın bu linkleri oynamak üzerine kurulu olmasından kaynaklanıyor.

Yukarıda verdiğimiz matrix'i, çifte linkli listeye dönüştürürken, her sütun için, ColumnNode adında özel bir node ekleniyor. Bu nodda, o sütunun adı ve o sütundaki node sayısı gibi bilgiler tutuluyor. İlk sütunun solunda ise, h adında özel bir nod var. Bu nod, algoritmanın başlangıç noktası. Bu nodların birbirine bağlanış şekli böyle:

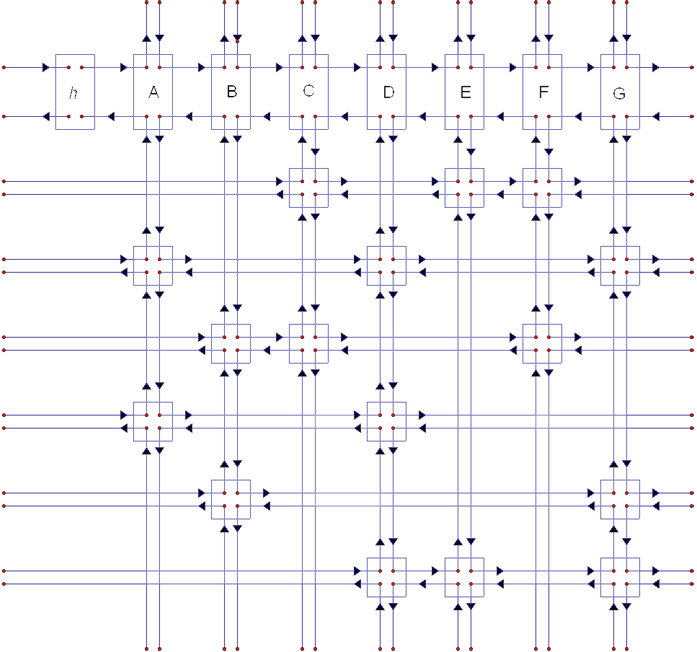
Knuth Dancing Links Exact Cover Matrix
Kaynak: http://www.ocf.berkeley.edu/~jchu/publicportal/sudoku/sudoku.paper.html

Algoritma şu şekilde işliyor:

fonksiyon çöz(matrix, çözümler):

  eğer bütün sütunlar matrix'den çıkarılmışsa, çözümleri döndür

  sütun := sıradakisütun()
  seç(sütun)
  sütun altındaki her node için:
      çözümler.ekle(node)
      bu nodun sağındaki nodların bulunduğu sütunları seç
      çöz(matrix, çözümler) # recursive bir şekilde matrix'in geri kalanı çözülüyor
      çözümler.çıkar(node)
      sağdaki seçilmiş sütunları seçimini iptal et.

  sütun seçimini iptal et.

Yukarıdaki çöz metodu, recursive, backtracking, depth-first bir algoritma. Backtrack, çıkarılmış node'ları geri ekleme ile sağlanıyor. Yukarıda da bahsettiğimiz gibi, bu ekleme çıkarma çok kolay bir işlem, bu yüzden algoritma bu kadar verimli.

Yukarıdaki pseudo-kod yeterince açıklayıcı olamamış olabilir. O yüzden bir de sözlü olarak açıklayayım. Hatırlarsanız, matrix içindeki sütunlar, karşılamamız gereken gereksinimleri, satırlar ise, bu gereksinimlerin biri veya birkaçını sağlayan seçenekleri gösteriyordu. Algoritma önce bir gereksinim seçiyor, ve bunu matrix'den kaldırıyor. Bunun matrix'den kaldırılması, bu gereksinimin sağlanmış olduğunu anlamına geliyor diye düşünebiliriz. Algoritma ardından, bu sütun altındaki nodları sırasıyla ilerliyor. Bu sütun altındaki her bir node, sütunda temsil edilen gereksinimin karşılanabileceği farklı bir seçenek. Bu seçeneklerden biri çözümler listesine eklendiğinden, o seçeneğin sağladığı diğer gereksinimler de matrix içerisinden kaldırılıyor. Sonra, recursive bir şekilde matrix tekrar işleme sokuluyor. Recursion tamamlandıktan sonra, yapılan şeyler geri alınıyor, bir sonraki nod çözümlere eklenip, böylece devam ediliyor.

Bir de örnek yapalım;

   A B C D E
1| 1 0 1 0 0
2| 1 0 0 1 0
3| 0 1 0 1 1

Algoritma, önce A sütununu kaldırarak başlayacak. İçinde 1 bulunan satırları sırasıyla çözümlere ekleyecek. Önce 1. satırı ekledi diyelim. Böylece, C sütununu da seçmiş oldu. Şimdi, geriye kalan matrix üzerinde arama yapacak

   B D E
3| 1 1 1

Geriye sadece 3. satır kaldı. İkinci satır da silindi, çünkü, A seçeneğini sağlayan birden fazla satırı aynı anda seçemeyiz. Bu adımda, 3. satırı seçmek bütün gereksinimleri sağlıyor. Dolayısıyla, (1 ve 3) ilk sonuç olarak döndü. Algoritma bu noktada, backtrack edip, A sütununu seçtiğimiz noktaya dönüyor.

   A B C D E
1| 1 0 1 0 0
2| 1 0 0 1 0
3| 0 1 0 1 1

Şimdi sırada satır ikiyi seçip devam etmek var.

   B C E
3| 1 0 1

Geriye sadece tek bir satır kaldı, ancak bu satır geriye kalan gereksinimlerimizi karşılamadı. Dolayısıyla bir sonuç döndüremedik. Algoritma bu noktada, başa dönüp, diğer sütunları seçerek aynı şeyleri deneyecek.

Sudoku

Gelelim, bütün bunların sudoku ile bağlantısına. Eğer sudoku'yu bir exact cover problemine dönüştürürsek, bu algoritmayı kullanarak istediğimiz sudokuyu çözebiliriz. Hatırlarsanız, kullandığımız matrix'de gereksinimler ve seçenekler vardı. Peki sudoku için gereksinimlerimiz nedir?

  • Her hücre'de, birden dokuza kadar bir sayı, ve sadece bir sayı olmalı. (81 hücre olduğundan 81 gereksinim)
  • Her satırda, birden dokuza kadar her sayıdan birer tane olmalı. (9 hücre x 9 sayı = 81 gereksinim)
  • Her sütunda, birden dokuza kadar her sayıdan birer tane olmalı. (9 hücre x 9 sayı = 81 gereksinim)
  • Her 3x3 lük bölgede, birden dokuza kadar her sayıdan birer tane olmalı. (9 hücre x 9 sayı = 81 gereksinim.)

Toplamda, bir sudoku oyununda, sağlanması gerekn 324 gereksinim var. Peki elimizdeki seçenekler neler?

Örneğin, 1.satır 1.sütunda 1 sayısının olması bir seçenek. Aynı hücrede 2 olması ayrı bir seçenek. Dolayısıyla, her hücre için, 9 seçeneğimiz var. 9x9'luk bir sudoku tahtasında, 81 hücre olduğu için, 9x81=729 farklı seçeneğimiz var.

Her bir seçenek, 4 gereksinimi karşılayacak. Örneğin, 1. satır, 1. sütunda 1 olması seçeneği:

  • O hücrede bir sayı bulunması gereksinimini
  • O satırda 1 bulunması gereksinimini
  • O sütunda 1 bulunması gereksinimini
  • 0 3x3lük bölgede 1 bulunması gereksinimini

Evet, sudoku çözmek için, önce bu matrix'i oluşturmak gerekiyor. Ancak, bu matrix'i oluşturmaya başlamadan önce, bunu Python'da nasıl kodlayabileceğimizi bir düşünelim. Bildiğiniz üzere, Python daha üst seviye bir programlama dili ve bu dildeki veri yapıları, C'ye göre farklı. İnternette, algorithm X'in, Python ile 30 satırda yazılmış şöyle bir versiyonunu buldum:

def solve(X, Y, solution=[]):
    if not X:
        yield list(solution)
    else:
        c = min(X, key=lambda c: len(X[c]))
        for r in list(X[c]):
            solution.append(r)
            cols = select(X, Y, r)
            for s in solve(X, Y, solution):
                yield s
            deselect(X, Y, r, cols)
            solution.pop()
def select(X, Y, r):
    cols = []
    for j in Y[r]:
        for i in X[j]:
            for k in Y[i]:
                if k != j:
                    X[k].remove(i)
        cols.append(X.pop(j))
    return cols
def deselect(X, Y, r, cols):
    for j in reversed(Y[r]):
        X[j] = cols.pop()
        for i in X[j]:
            for k in Y[i]:
                if k != j:
                    X[k].add(i)

Burada, satır ve sütunlar, bir çift-link liste yerine, Python sözlüklerinde tutulmuş. Örneğin, en başta verdiğim şu örneği düşünelim:

X = {1,2,3,4,5}
S = {{1,3},{1,4},{2,4,5}}

Bunu, yukarıdaki yöntem, bunu şu hale getiriyor;

X = {1:{'A','B'},
     2:{'C'},
     3:{'A'},
     4:{'B','C'}
     5:{'C'}}

Y = {
    'A':[1,3],
    'B':[1,4],
    'C':[2,4,5]

Satırlar ve sütunlar ayrı ayrı Python sözlükleri içerisindeler. Satırlardan sütunlara hızlıca erişmek için Y, sütunlardan satırlara erişmek için X sözlüğünü kullanıyor. Algoritmanın geri kalanı algorithm X ile aynı.

Python ile yazılmış sudoku çözücüye, her zamanki gibi gist üzerinden ulaşabilirsiniz.

Yukarıdaki linkteki Python kodlarını da açıklayacaktım ama, bugünlük yoruldum yazmaktan. Belki ileriki bir zamanda, benchmarklarla birlite açıklarım o kodları da.

Referanslar