Ne zamandır fraktal geometri meraklısı bir insanım. Python'da turtle kütüphanesini olduğunu farkedince (bunca zamandır nasıl görmediysem...) ilk iş
aklıma fraktal çizmek geldi. Blog'dan da paylaşayım istedim.
Öncelikle, turtle nedir ondan bahsedeyim biraz. Bu kütüphane ekrandaki bir kaplumbağa'ya (temsili) komutlar vermenizi sağlıyor. Örneğin, ileri git, geri
git, sağa dön sola dön gibi komutlar veriyorsunuz. Kamlumbağanın gittiği yol ekranda çizgi olarak görülüyor.
Örneğin ekrana bir kare çizmek için, 4 kere 100 birim ilerle, 90 derece sola dön komutunu verebilirsiniz. Python'da bunu yapmak için, turtle kütüphanesini
kullanıyoruz.
|
from turtle import Turtle, screen
|
|
|
|
wn = screen() # ekranı kontrol etmemizi sağlıyor
|
|
|
|
t = Turtle() # bir adet kaplumbağa oluşturduk.
|
|
|
|
for i in range(4):
|
|
t.forward(100) # kaplumbağa 100 birim ilerlesin
|
|
t.left(90) # 90 derece sola dönsün
|
|
|
|
wn.exitonclick() # ekrana tıklanınca ekran kapansın
|
Şimdi de siz deneyin : Ekrana bir üçgen çizin!
Fraktal çizmek için ise, en basit yol, recursive fonksiyon kullanmak. Mesela, bir ağaç çizelim;
|
from turtle import Turtle, Screen
|
|
|
|
wn = Screen()
|
|
|
|
def tree(length,t):
|
|
if length > 5:
|
|
t.forward(length) # ileri git
|
|
t.right(40) # sağa dön
|
|
tree(length-15,t) # daha küçük bir ağaç çiz
|
|
t.left(80) # sola dön
|
|
tree(length-15,t) # daha küçük bir ağaç çiz
|
|
t.right(40) # Başladığın açıya geri dön
|
|
t.backward(length)# Başladığın noktaya geri dön
|
|
|
|
|
|
t = Turtle()
|
|
t.left(90) # Yukarıya doğru çizmek için
|
|
t.speed(0) # en hızlı animasyon
|
|
|
|
tree(100,t)
|
|
|
|
wn.exitonclick()
|
Şöyle bir resim oluşması gerekiyor;
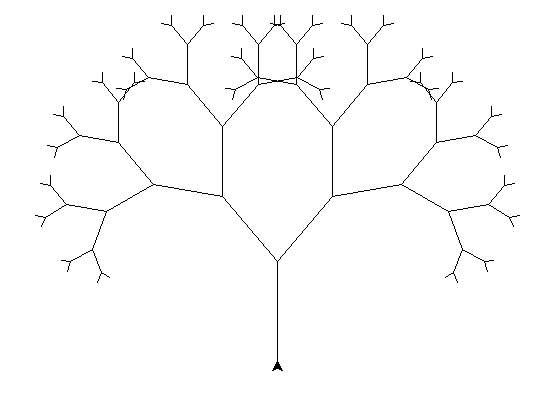
Her ne kadar recursive fonksiyonlar basit olsa da, şekiller karmaşıklaştıkça uygulaması daha zor olabilir. Bunun yerine, fraktal çizmek
için L-Sistemi denilen bir sistem kullanacağız. Eğer fraktal meraklısı bir insansanız, L-sistemini zaten duymuşsunuzdur. Bilmeyenler için kısaca
bahsetmek gerekirse; elimizde belli bir karakter string'i var. Bunu belli kurallar çerçevesinde, giderek kendi içerisinde büyütüyoruz. Örnek verelim;
Başlangıç: A
Kurallar : A -> AB
B -> A
Adımlar:
1) A
2) AB
3) ABA
4) ABAAB
5) ABAABABA
6) ... Böyle gidiyor
Peki, bunun fraktallarla ne alakası var? Bildiğiniz gibi (bildiğinizi varsayıyorum) fraktallar kendi içinde yenilenen segmentlerden oluşuyor. İşte bu kendi
içinde yenilenmenin kuralını, L-Sistemi ile belirleyip, kaplumbağa'ya o şekili çizdiriyoruz.
Örnek olarak, Koch Snowflake şeklinin ilk 3 adımına bakalım.
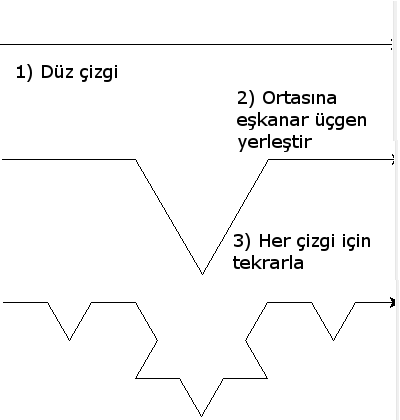
Evet, önce düz bir çizgi ile başladık, daha sonra bu çizgiyi 3'e bölüp, ortadaki kısmı silip, üstüne bir eşkanar üçgen yerleştirdik. Daha sonra da, her çizgi bölümü
için, bunu tekrarlıyoruz. Eğer aynı işlemi 6. adıma kadar devam edersek, şöyle bir şekil elde ediyoruz.

Şimdi de bu işlemi, L-Sisteminde nasıl ifade edebileceğimize bakalım;
Başlangıç: f
Kurallar: f -> f+f--f+f
Burada, f aksiyonu ileri git, + aksiyonu 60 derece sola dön, - ise, 60 derece sağa dön manasına geliyor. Şimdi, bu kurallara göre, istediğimiz derinlikle
L-dizisi oluşturacak bir fonksiyon yazalım.
|
def make_l_string(start, rules, depth):
|
|
string = start
|
|
for _ in range(depth):
|
|
string = "".join(rules[x] for x in string)
|
|
return string
|
|
|
|
koch_rules = {
|
|
'f' : 'f+f--f+f',
|
|
'+' : '+',
|
|
'-' : '-'
|
|
}
|
|
|
|
print make_l_string("f", koch_rules, 3)
|
f+f--f+f+f+f--f+f--f+f--f+f+f+f--f+f+f+f--f+f+f+f--f+f--f+f--f+f+f+f--f+f--f+f--f+f+f+f--f+f--f+f--f+f+f+f--f+f+f+f--f+f+f+f--f+f--f+f--f+f+f+f--f+f
Buradaki ana fikirden yola çıkarak, farklı fraktallar çizmek için kullanılabilecek python sınıfları hazırladım, kodlar aşağıda;
Güncelleme: 12.07.2014 10:55 Kodlara biraz daha çeki düzen verdim.
|
# -*- coding: utf-8 -*-
|
|
import turtle
|
|
|
|
class Lindenmayer(turtle.Turtle):
|
|
"Bracketed L System"
|
|
|
|
syms = {
|
|
"F":"gforward",
|
|
"f":"jforward",
|
|
"+":"tright",
|
|
"-":"tleft",
|
|
"A":"gforward",
|
|
"B":"gforward",
|
|
"U":"penup",
|
|
"D":"pendown",
|
|
"[":"push_stack",
|
|
"]":"pop_stack",
|
|
"1":"color1", # black by default
|
|
"2":"color2", # red by default
|
|
"3":"color3", # green by default
|
|
"4":"color4", # blue by default
|
|
}
|
|
|
|
def draw(self):
|
|
|
|
self.hideturtle() # to speed up the drawing
|
|
for x in self.string:
|
|
try:
|
|
getattr(self,Lindenmayer.syms[x])()
|
|
except KeyError:
|
|
"For actions that don't do anything"
|
|
pass
|
|
|
|
def gforward(self): self.forward(self.d)
|
|
|
|
def jforward(self):
|
|
"Go forward, but don't draw"
|
|
self.penup()
|
|
self.forward(self.d)
|
|
self.pendown()
|
|
|
|
def tleft(self):
|
|
"Turn left by degrees"
|
|
self.left(self.a)
|
|
|
|
def tright(self):
|
|
"Turn right by degrees"
|
|
self.right(self.a)
|
|
|
|
def push_stack(self):
|
|
"push state to stack"
|
|
self._stack.append((self.pos(), self.heading()))
|
|
|
|
def pop_stack(self):
|
|
"pop and restore state"
|
|
|
|
pos, heading = self._stack.pop()
|
|
self.penup()
|
|
self.setpos(pos)
|
|
self.setheading(heading)
|
|
self.pendown()
|
|
|
|
def color1(self):
|
|
self.pencolor("#000000")
|
|
|
|
def color2(self):
|
|
self.pencolor("#ff0000")
|
|
|
|
def color3(self):
|
|
self.pencolor("#00ff00")
|
|
|
|
def color4(self):
|
|
self.pencolor("#0000ff")
|
|
|
|
def fix_rules(self):
|
|
"Add unspecified conversions. They stay the same"
|
|
|
|
parts = set("".join(self.rules.keys() + self.rules.values()))
|
|
|
|
for x in parts:
|
|
if not x in self.rules.keys():
|
|
self.rules[x] = x
|
|
|
|
def init(self, depth, speed=0):
|
|
"Prepare required variables before draw"
|
|
|
|
self._stack = []
|
|
self.speed(speed)
|
|
|
|
self.depth = depth
|
|
|
|
string = self.begin
|
|
|
|
self.fix_rules()
|
|
|
|
for _ in xrange(depth):
|
|
|
|
string = "".join(self.rules[x] for x in string)
|
|
|
|
self.string = string
|
|
|
|
self.after_init()
|
|
|
|
def after_init(self):
|
|
"Extra stuff, executed right after init function"
|
|
pass
|
|
|
|
#### Begin L-System Equations ###
|
|
|
|
class koch(Lindenmayer):
|
|
|
|
rules = {'F':'F-F++F-F'}
|
|
begin = "F"
|
|
a = 60
|
|
|
|
def after_init(self): self.d = max(400 / 3 ** self.depth,1) # set distance appopropiate to complexity
|
|
|
|
|
|
class square_koch(Lindenmayer):
|
|
|
|
rules = {'F':'F-F+F+F-F'}
|
|
begin = "F"
|
|
a = 90
|
|
def after_init(self): self.d = max(400 / 3 ** self.depth,1)
|
|
|
|
|
|
class sierpinsky(Lindenmayer):
|
|
|
|
rules = {'A':'B-A-B', 'B':'A+B+A'}
|
|
begin = 'A'
|
|
a = 60
|
|
|
|
def after_init(self): self.d = max( 300 / 2 ** self.depth,1)
|
|
|
|
class fibonacci_tree(Lindenmayer):
|
|
|
|
rules = {'A':'AA', 'B': 'A[-B]+B'}
|
|
begin = "B"
|
|
a = 30
|
|
|
|
def after_init(self): self.d = max(300 / 2**self.depth,1); self.left(90)
|
|
|
|
class dragon_curve(Lindenmayer):
|
|
|
|
rules = {'x':'x+yF', 'y': 'Fx-y'}
|
|
begin = "Fx"
|
|
a = 90
|
|
|
|
def after_init(self): self.d =max( 300 / 1.5 ** self.depth, 1)
|
|
|
|
|
|
|
|
class fractal_plant(Lindenmayer):
|
|
|
|
rules = {'X':'F-[[X]+X]+F[+FX]-X', 'F': 'FF'}
|
|
begin = "X"
|
|
a = 25
|
|
|
|
def after_init(self):
|
|
self.d = max(120 / 1.9 ** self.depth, 1)
|
|
self.left(90)
|
|
self.pensize(3)
|
|
|
|
if __name__ == "__main__":
|
|
|
|
from time import sleep
|
|
wn = turtle.Screen()
|
|
|
|
things_to_draw = (
|
|
(koch,3),
|
|
(square_koch,3),
|
|
(sierpinsky,6),
|
|
(fibonacci_tree,5),
|
|
(dragon_curve,10),
|
|
(fractal_plant,5),
|
|
)
|
|
|
|
for c, x in things_to_draw:
|
|
wn.clearscreen()
|
|
f = c()
|
|
f.init(x)
|
|
f.draw()
|
|
sleep(1)
|
|
|
|
wn.exitonclick()
|
Bunlar da sonuçlarımız (Büyük Hali İçin Tıklayınız);
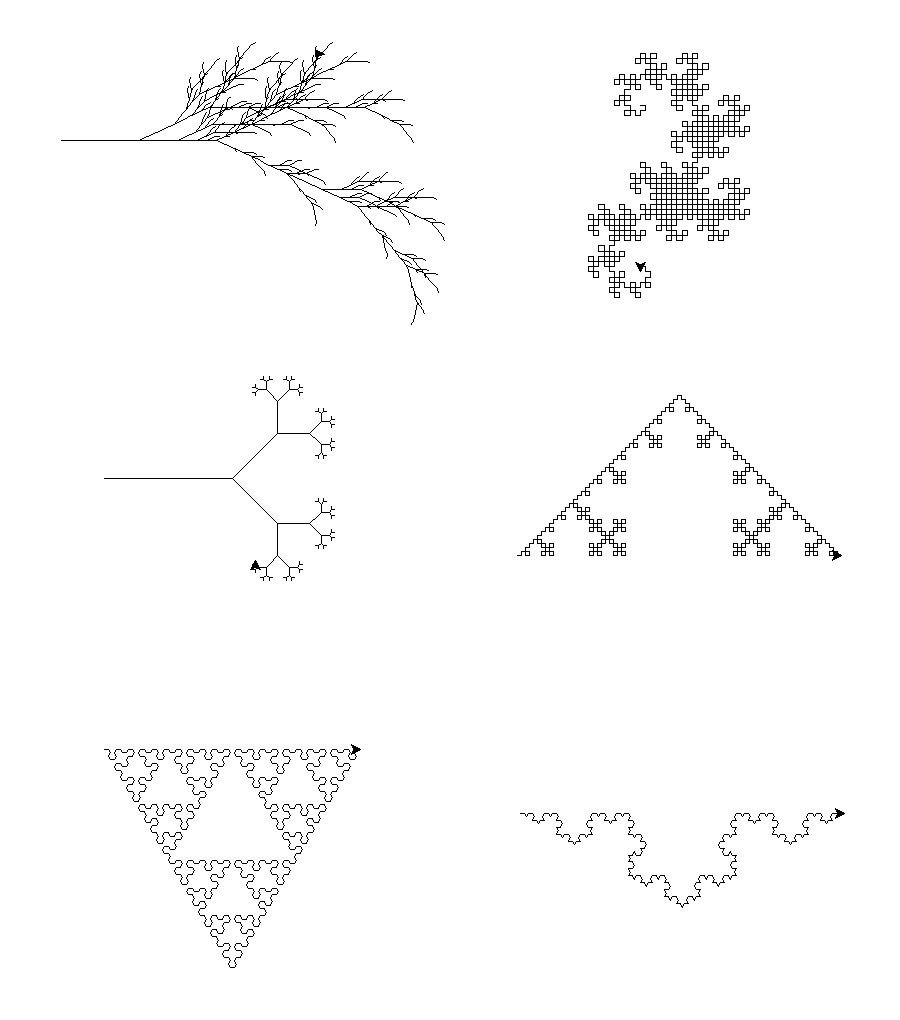
Peki ya bundan sonra? Daha farklı fraktal şekiller çizmek için yeni L-sistemi kuralları araştırılabilir. Eğer yeni şekiller eklersem, onları da daha sonra paylaşırım.




