(Euler 15) Izgara Üzerindeki Yollar

2x2 ızgaranın sol üst köşesinden başlayarak, ve sadece sağa veya aşağıya hareket ederek, sağ alt köşeye tam olarak 6 yol vardır.

20x20 ızgarada bu şekilde kaç adet yol vardır?

from math import factorial as f
print(f(40)/f(20)**2)

Problemin çözümü bu kadar basit olsa da, çözüme ulaşmak o kadar da kolay olmadı. Her ne kadar sırasıyla tüm yolları tarayıp saymak en kolay yöntem gibi görünse de, 20X20 bir ızgarada bu yöntem çok uzun sürecektir. Rivayet odur ki, ikinci dünya savaşı yıllarında başlatılan bir program, bugün hala 20X20 ızgarada gidilebilecek yolları hesaplıyormuş. (Öyle bir rivayet yok, ben uydurdum.) Ancak, probleme doğru açıdan bakınca, çok daha kolay bir yöntem kendini belli ediyor. Bu soruyu, doğru cevabı etkilemeyecek bir şekilde, permüstasyon sorusuna dönüştürebiliriz.

Bu problemi permüstasyon problemine dönüştürebilmek için şuna dikkat etmek gerekiyor; 2X2 bir ızgarada sol üst köşeden sağ alt köşeye gidebilmek için, tam iki kere sağa ve tam iki kere aşağıya doğru hareket etmeniz gerekiyor. Seçilebilecek yollar arasındaki tek fark, aşağı ve sağa doğru hareketlerin hangi sırayla yapıldığı. Sağa atılacak adımları S, aşağıya atılacak adımları ise A ile ifade edersek, 2X2 ızgarada seçilebilecek 6 farklı yol şunlardır; "SSAA", "SASA", "SAAS", "ASSA", "ASAS", "AASS". Dolayısıyla, {A, A, S, S} kaç farklı şekilde dizilebilir sorusunua cevap verdiğimizde, 2X2 ızgarada sol üst köşeden sağ alt köşeye kaç farklı yoldan gidilebilir sorusuna da cevap vermiş oluyoruz. Tekrarlı permüstasyon formülü ile \(\frac{4!}{2! \cdot 2!} = 6\) olarak sonucu teyit edebiliriz. Aynı yöntemle, \(m \times n\) bir ızgarada, bir köşeden karşı köşeye gitmek için seçilebilecek yol sayısını aşağıdaki Python fonksiyonu ile hesaplayabiliriz.

from math import factorial as f
def lattice(m, n):
    return f(m+n) / (f(m) * f(n))

Bu problemi çözmek için Pascal Üçgeni de kullanabiliriz. Bu yöntemi internette rastladığım bir blog yazısında gördüm. Ana fikri anlamak için, 3X3 ızgarada herhangi bir köşeden, sağ alt köşeye gitmek için kaç farklı yoldan geçebileceğimize bir bakalım.

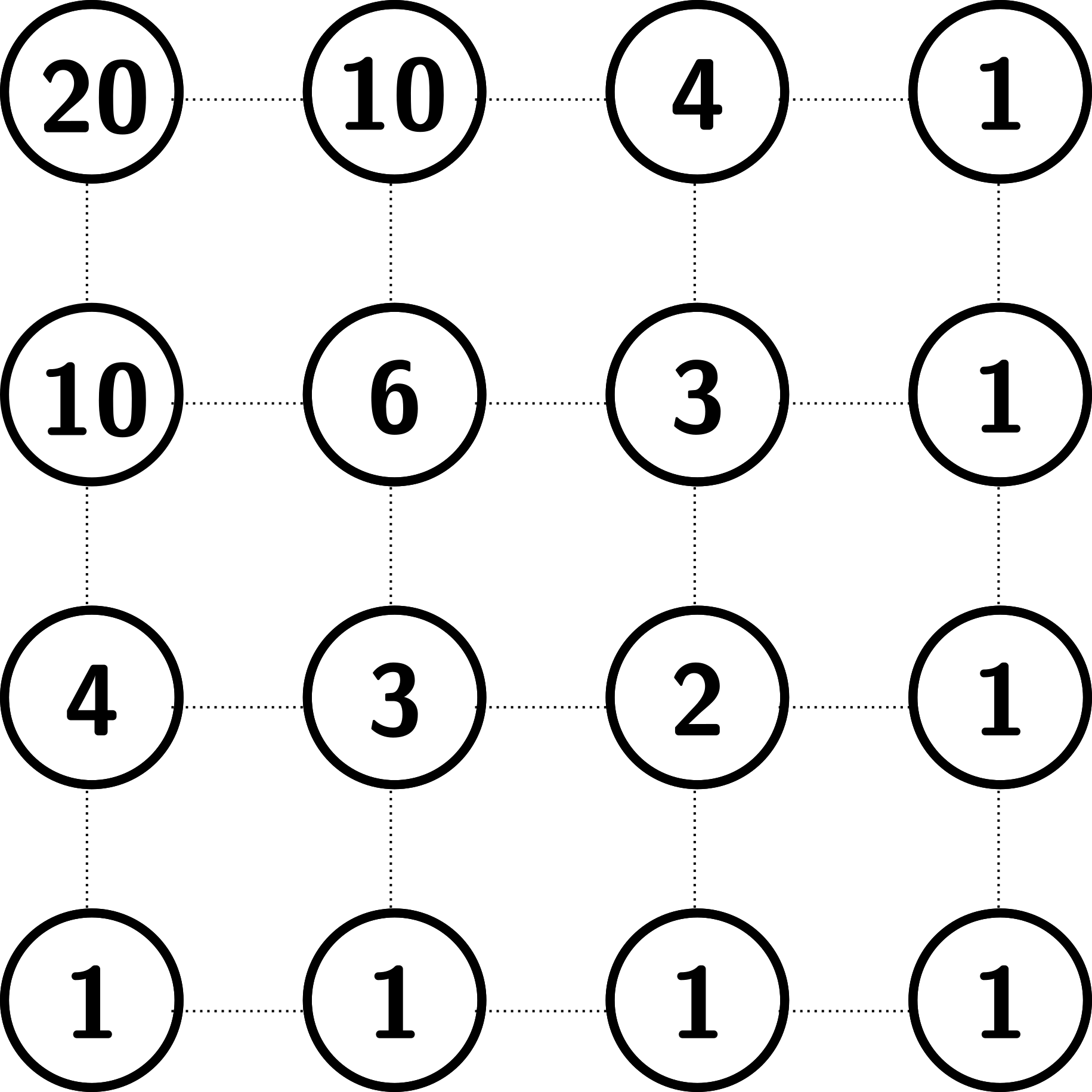
g5028

Eğer ızgaranın en sağ hizasındaysanız, tek seçeneğiniz aşağıya doğru devam etmek. Aynı şekilde, eğer ızgaranın el altındaysanız, tek seçeneğiniz sağa doğru devam etmek. Bu nedenle, ızgaranın sağ ve alt hizasındaki köşelerde 1 yazılı. Eğer üzerinde 2 yazılı köşedeyseniz, sona ulaşmak için 2 farklı yol tercih edebilirsiniz. Ya aşağıdan sağa doğru, ya da sağdan aşağı doğru gidebilirsiniz. Eğer alttan ikinci sırada, üzerinde 3 yazan köşeye bakarsanız, işler ilginçleşmeye başlıyor. Izgaranın bu köşesinden sağa doğru gidilirse, sona ulaşmak için iki farklı yol seçilebilir. Eğer aşağı doğru gidilirse, sonuca tek bir yoldan ulaşılabilir. Yani, sağa gittikten sonraki 2 seçenek ve aşağı gittikten sonraki tek seçenekle birlikte, toplam 3 seçeneğimiz olacak. Aynı şekilde, alttan ikinci sıradaki, üzerinde 4 yazılı köşede, ya aşağıya gitmeyi ya da sağdaki 3 seçenekten birini tercih edebiliriz. Bu durumda toplam 4 seçeneğimiz olacak. Yani, herhangi bir köşedeki toplam seçenek sayımız, sağdaki ve alttaki köşelerin seçenek sayısının toplamı olacak. Eğer yukarıdaki resmi, sağ alt köşe üste gelecek şekilde döndürürseniz, bir Pascal Üçgeni elde ettiğimizi göreceksiniz.

Orjinal problemi Pascal üçgeni kullanarak çözmek için, istediğimiz sonucu üçgenin neresinde bulacağımızı tespit etmemiz gerekiyor. Adet olduğu üzere saymaya sıfırdan başlarsak, 1X1 ızgara için çözüm Pascal Üçgenin ikinci satır, birinci sütununda (2,1), 2X2 için çözümü (4,2) koordinatında bulabilirz. Dolayısıyla, Pascal Üçgeni'nde (40,20) deki değeri bulduğumuzda, soruyu da çözmüş olacağız. Pascal üçgenindeki herhangi bir noktayı bulmak için bir formül olsa da, önce döngü ile yapalım.

def pascal(r,c, cache={(0,0): 1}):
    if (r,c) in cache:
        return cache[(r,c)]
    if c < 0:
        return 0
    if c > r:
        return 0
    cache[(r,c)] = pascal(r-1, c-1) + pascal(r-1,c)
    return cache[(r,c)]
print(pascal(2,1))
print(pascal(4,2))
print(pascal(6,3))
print(pascal(40, 20))

Yukarıdaki gibi bir çözüm de bir hayli hızlı sonuç veriyor. cache isimli sözlüğe neden ihtiyacımız olduğunu anlamadıysanız, (Euler 2) Çift Fibonacci Sayıları yazısındaki, "Bonus: Özyinelemeli versiyon, sorunları ve çözümleri" başlığı altındaki bölümü okumanızı tavsiye ederim.

Pascal üçgeni üzerinde aradığımız değerin bulunduğu satıra \(r\), sütuna da \(c\) dersek, istediğimiz değeri \(\frac{r!}{c!(r-c)!}\) formülü ile bulabiliriz. Formül bir yerden tanıdık geliyor. Tekrarlı permüstasyon formülü bu. Bu soruyu çözmeden önce, Pascal Üçgeni ile belki 20 yıldır muhatap olmamıştım. Binom açılımı için kullanıldığını biliyordum ama, kombinasyon ile ilişkisini yeni öğrendim. Biraz dikkat edince, binom açılımdaki katsayıların kombinasyon hesabıyla tespit edilmesi çok doğal geliyor. Şimdiye kadar farkedemediğime hayret ettim doğrusu.

Her ne kadar yazının başında tüm yolları taramanın çok uzun süreceğini iddia etmiş olsam da, taramayı yapmanın yanlış yolları olduğu gibi, doğru yolları da var. Örneğin, yukarıdaki resimdeki gibi bir ızgarayı sondan başa doğru çok hızlı bir şekilde tarayabiliriz. Bu tarz şeyleri C ile yazmak daha keyifli geliyor, o yüzden öyle yaptım.

#include <stdint.h>
#include <stdio.h>
#include <limits.h>
#ifndef GRIDSIZE
#define GRIDSIZE 20
#endif
#define WILL_OVERFLOW(x,y) (x > ULLONG_MAX - y)
unsigned long long grid[GRIDSIZE+1][GRIDSIZE+1];
unsigned long long solve()
{
    int i, k;
    unsigned long long t1, t2;
    // Kenarlari 1 ile doldur
    for(i = 0; i < GRIDSIZE+1; i++)
    {
        grid[0][i] = 1;
        grid[i][0] = 1;
    }
    for(i = 1; i < GRIDSIZE+1; i++)
    {
        for(k = 1; k < GRIDSIZE+1; k++)
        {
            t1 = grid[i-1][k];
            t2 = grid[i][k-1];
            if(WILL_OVERFLOW(t1, t2))
            {
                printf("Sayilar cok buyuk, hesaplanamadi\n");
                return -1;
            }
            grid[i][k] = t1 + t2;
        }  
    }
    return grid[GRIDSIZE][GRIDSIZE];
}
main(int argc, char const *argv[])
{
    printf("%dX%d izgarada %llu yol var.\n", GRIDSIZE, GRIDSIZE, solve());
    return 0;
}

20X20'lik ve 30x30'luk ızgaraları yukarıdaki programla hesaplayabiliyorum. 35x35 olarak denediğimde, 64-bit integer'a sonuç sığmadı.

Son olarak, doğru cevabın sayısal değeri de çok enteresan. Yaklaşık olarak 138 milyar. Dünya nüfusunun 7-8 milyar civarı olduğunu düşünürsek, dünyadaki herkesi 20X20 ızgarada farklı yollardan karşı köşeye geçerse, geriye 130 milyar ihtimal daha kalıyor. Bu kadar büyük olacağını beklemezdim.

Gelecek Problem

\(2^{15} = 32768\) ve rakamları toplamı \(3 + 2 + 7 + 6 + 8 = 26\).

\(2^{1000}\) sayısının rakamları toplamı kaçtır.